유형9. 대금 정산
서너 명이 각각 돈을 지불하고 물건을 산 다음, 최종적으로 지불 금액이 같도록 정산하는 문제이다.
여기에 서로가 돈을 빌리는 경우가 있어 문제가 복잡해지는 경우도 있다.
Point 1: 한 명 당 지불액을 먼저 확인할 것!
세 명이 각각 2000엔, 3000엔, 7000엔의 물건을 구매 ⇒ 한 명 당 지불액은 4000엔
Point 2: 돈을 빌린 경우가 있을 경우, 먼저 빌린 금액에서 더하거나 빼서 정산할 것!
P가 Q에게 3000엔 빌려주었고, R에게 1000엔을 빌렸을 경우 ⇒ P의 현재 정산액은 +2000엔
암산으로 문제를 풀 경우 복잡해지기 때문에, 이런 식으로 정리를 해나가면서 풀면 될 것 같다.
유형9-1
P、Q、Rの3人はキャンプに行くための買い物に出かけた。 Pは2300円分の食べ物の材料を、Qは3700円分の調理器具を、Rはテントを買った。 後日、3人が同額ずつ負担するために、Rに対し、Pは2000円支払い、Qも600円支払った。 このとき、テントの代金はいくらか。
A 6200円
B 6300円
C 6400円
D 6500円
E 6600円
F 6700円
G 6800円
H 6900円
유형9-2
PはQに3000円貸しており、QはRに4000円貸しており、RはPに5000円貸している。
この3人が一緒に映画を見に行った。
映画の代金を全員同額ずつ負担したいが、ひとまずRが全員分の6000円を立て替えた。
3人の間の貸し借りを全て精算するにあたり、次の2つの方法を考えた。
① PがRに( ア )円支払い、QがRに( イ )円支払う。
② PがQに( ウ )円支払い、QがRに( エ )円支払う。
ただし、ア、イ、ウ、エに当てはまるものは正の整数であるものとする。ウとエに当てはまる数字はいくつか。
A ウ:2000円、エ:5000円
B ウ:2000円、エ:6000円
C ウ:3000円、エ:5000円
D ウ:3000円、エ:6000円
E ウ:4000円、エ:5000円
F ウ:4000円、エ:6000円
G ウ:5000円、エ:5000円
H ウ:5000円、エ:6000円
유형9-3
3兄弟のP、Q、Rは母の誕生日プレゼントにマフラーを買うことにした。 PはQから6000円を預かり、もともと7000円貸していたRからは12000円お金を預かって出かけた。 結局、Pは24000円のマフラーを買うことになった。
この後、3人の貸し借りがすべてなくなるよう代金の精算をすることとなった。 Rは「僕はPから7000円借りていて、12000円を預けたから、差額の半分の2500円返してくれるかな」と言い、 Pは「Qからは追加で2000円もらえるかな。プレゼント代は一人あたり8000円だから、預かった額との差を考えれば、それで帳尻が合うはず」と言った。 このように精算するとPはいくら得、または損をするか。
A 2500円損をする
B 3500円損をする
C 4500円損をする
D 5500円損をする
E 2500円得をする
F 3500円得をする
G 4500円得をする
H 5500円得をする
유형10. 요금 할인
물건을 한 번에 많이 구매할 때, 할인이 적용되는 경우가 있다. 이때의 총액을 구하는 문제.
간단한 유형으로, 방정식만 잘 세운다면 어렵지 않게 풀 수 있다.
유형10-1
あるネットワーク回線の月額使用料は、基本料金として3000円かかる。 また、100時間を超えると超過料金として1時間当たり20円の超過料金がかかる。 ある月の1時間当たりの平均料金が22円のとき、その月のネットワーク回線の使用時間は何時間か。
A 350時間
B 400時間
C 450時間
D 500時間
E 550時間
F 600時間
G 650時間
H 700時間
유형10-2
ある博物館の入館料は1人1000円だが、11人以上の団体には団体割引が適用される。 割引率は、11人目から30人目は20%引き、31人目以降は50%引きである。 この博物館を50人の団体で見学したとき、1人当たりの平均の入館料はいくらか。
A 720円
B 740円
C 760円
D 780円
E 800円
F 820円
G 840円
H 860円
유형10-3
あるホテルの宿泊料金は1人6500円である。 しかし、16人以上の団体の場合、15人を超える分については1人4500円に割引される。 40人の団体が、20人ずつ2回に分けて宿泊する場合と、全員で1回に宿泊する場合では、料金の総額はいくら異なるか。
A 29000円
B 30000円
C 31000円
D 32000円
E 33000円
F 34000円
G 35000円
H 36000円
유형11. 비율 계산
'~한 경우의 ~한 경우' 를 구하는 문제. 표 분석 문제에서도 자주 출제되는 유형이다.
유형11-1
ある日の国立博物館Pの訪問者数は8000人で、そのうち40%が女性の訪問者であった。男性の訪問者のうち、70%が20歳以上であった。20歳未満の訪問者は何人か。
A 720人
B 840人
C 960人
D 1080人
E 1200人
F 1320人
G 1440人
H 1560人
유형11-2
ある日の国立博物館Pの訪問者数は8000人で、そのうち40%が女性の訪問者であった。男性の訪問者は変わらず、女性の訪問者だけが1000人増えた場合、女性の訪問者は全体の何%となるか(必要なときは、最後に小数点以下第1位を四捨五入すること)。
A 46%
B 47%
C 48%
D 49%
E 50%
F 51%
G 52%
H 53%
유형11-3
イチゴ、抹茶、黒チョコ、白チョコの4種類のクッキーと平らな箱がある。 箱全体の20%の面積にイチゴクッキーを敷きつめた。残った面積の30%に抹茶クッキーを敷きつめ、更に残った面積には黒チョコクッキーと白チョコクッキーを2:3の割合で敷きつめたとき、 黒チョコクッキーの面積は箱全体の何%か(必要なときは、最後に小数点以下第1位を四捨五入すること)。
A 21%
B 22%
C 23%
D 24%
E 25%
F 26%
G 27%
H 28%
유형11-4
箱Pにはミカン、リンゴ、イチゴの個数がそれぞれ30%、50%、20%の割合で入っており、箱Qにはそれぞれ20%、40%、40%の割合で入っている。箱Qに入っている果物をすべて箱Pに移した。箱Qの果物を箱Pに移した後、リンゴとイチゴの数の比が4:3になった。箱Qに入っていた果物の数は、箱Qの中身を移す前の箱Pの何倍か。
A (1/2)倍
B (4/7)倍
C (3/5)倍
D (2/3)倍
E (3/2)倍
F (5/3)倍
G (7/4)倍
H 2倍
유형12. 분할 지불
한 상품을 할부로 계산할 때, 현시점에서 전체의 얼마만큼 지불하는가를 구하는 문제.
표 분석과 비율 계산과 마찬가지로 '~한 비율 중, ~한 비율' 을 계산하면 된다.
유형12-1
新しく印刷機を購入する。購入時に総額の1 / 5を支払い、残額を7回に均等に分割して支払う。分割払いの1回当たりの支払額は総額のどれだけにあたるか。ただし、利子はかからないものとする。
A 1/14
B 3/35
C 1/10
D 4/35
E 9/70
F 1/7
G 11/70
H 6/35
유형12-2
新しく液晶テレビを購入し、代金は3回に分けて支払うことにした。 初回は総額の1 / 6を支払った。2回目に初回の2 / 3を支払い、3回目に残額を全て支払うとき、3回目に支払う金額は初回のどれだけに当たるか。ただし、利子はかからないものとする。
A 19/6
B 10/3
C 7/2
D 11/3
E 23/6
F 25/6
G 13/3
H 9/2
유형12-3
新しくエアコンを購入する。購入時に価格の何割かを支払い、残額を8回に均等に分割して支払う。 このとき、分割手数料として残額の1 / 5を加えた額を8等分して支払うこととなる。頭金が購入価格の1 / 5のとき、分割払い1回あたりの支払い額は購入価格のどれだけにあたるか。
A 1/16
B 2/25
C 1/12
D 1/11
E 1/9
F 3/25
G 1/8
H 2/15
유형13. 장치와 회로
'블랙박스' 라고 불리는 수치를 변환하는 장치를 연결한 회로에 있어서, 입출력되는 숫자를 구하는 문제이다.
변환되는 규칙을 찾으면 간단하게 풀 수 있는 문제들이다.
유형13-1
入力信号である0、1を次のようなルールで変換し出力する装置P、Q、Rがある。
Pは、入力信号Xを逆の信号Yに変えて出力する。(例えば、入力信号が0のときは、1を出力する。)
Qは、2つの入力信号がともに0のときは0を出力し、2つの信号のうち少なくとも一方が1ならば1を出力する。
Rは、2つの入力信号がともに1のときは1を出力し、2つの信号のうち少なくとも一方が0ならば0を出力する。
これらの装置をつなぎ、下図のような回路を作り、X1、X2、X3にア、イ、ウの組合せで信号を入力した。 ア、イ、ウのうち、Yが1になるものはどれか。
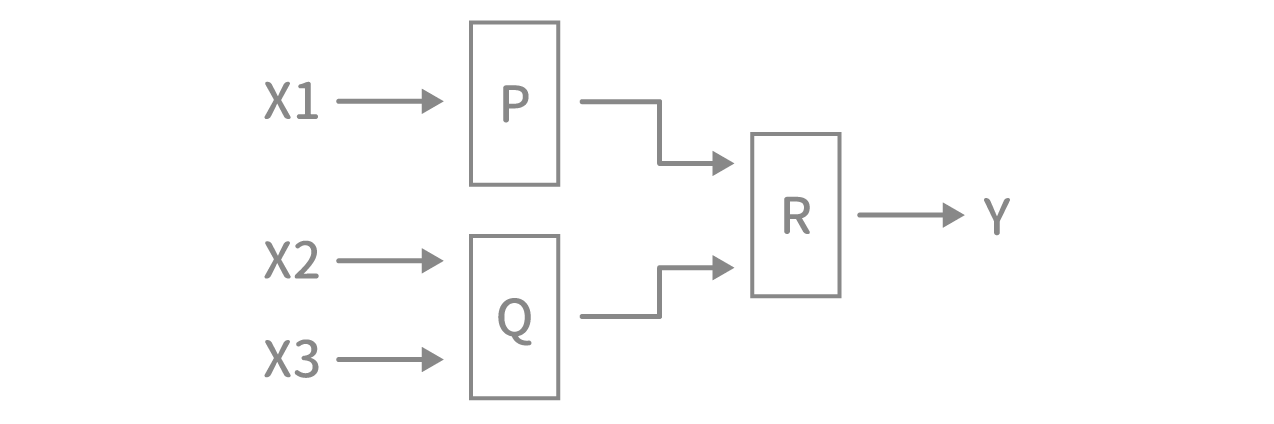
| 組合せ | X1 | X2 | X3 |
| ア | 0 | 0 | 1 |
| イ | 0 | 1 | 1 |
| ウ | 1 | 1 | 1 |
A アだけ
B イだけ
C ウだけ
D アとイの両方
E アとウの両方
F イとウの両方
G アとイとウのすべて
H アとイとウのいずれでもない
유형13-2
入力信号である0、1を次のようなルールで変換し出力する装置P、Q、Rがある。
Pは、入力信号Xを逆の信号Yに変えて出力する。(例えば、入力信号が0のときは、1を出力する。)
Qは、2つの入力信号が、ともに0かともに1ならば0を出力し、2つの信号のうち片方が0でもう片方が1ならば1を出力する。
Rは、2つの入力信号がともに1のときは1を出力し、2つの信号のうち少なくとも一方が0ならば、2 / 3の確率で1を出力し、1 / 3の確率で0を出力する。
これらの装置をつなぎ、下図のような回路を作り、X1 = 1、X2 = 0 、X3 = 1、X4 = 1の組合せで信号を入力した。Yが1となる確率はいくらか。
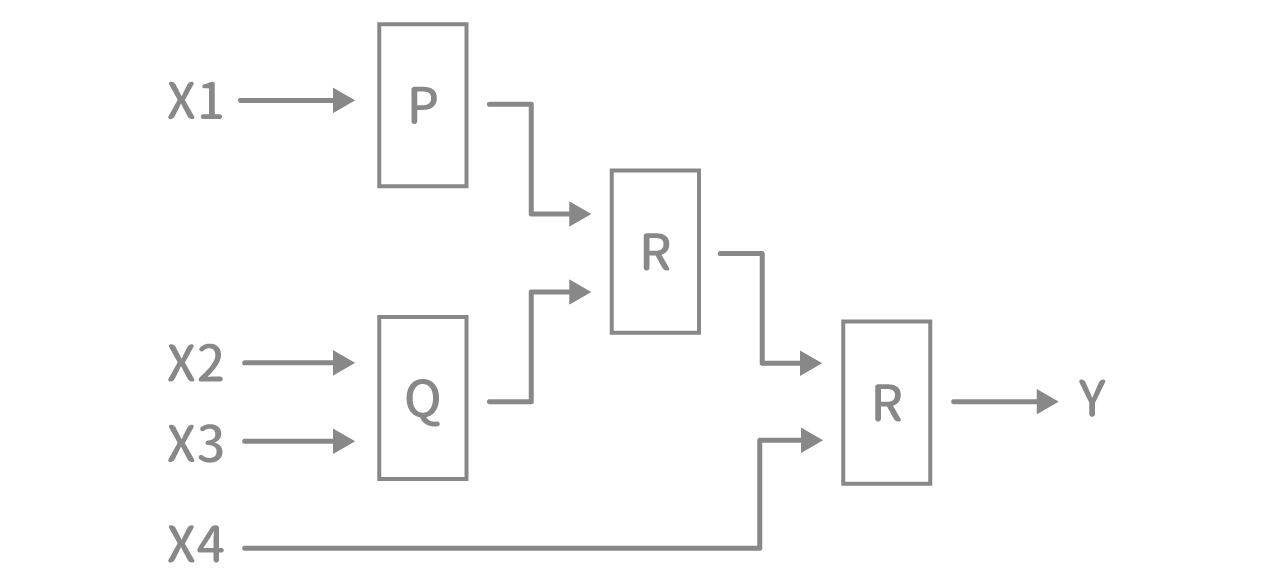
A 1/9
B 2/9
C 1/3
D 4/9
E 5/9
F 2/3
G 7/9
H 8/9
유형14. 사물의 흐름과 비율
사람이나 물건의 흐름을 수식으로 나타낸 도표가 나오는 문제이다.
처음 볼 때는 어렵게 보일 수 있지만, 사물이 흘러가는 길을 연결하는 것만으로도 간단하게 풀 수 있다.
유형14-1
次の図は、S会場とT会場とV会場とX会場からZ会場に進んだ人を表したものである。
(基本ルールは省略します。)
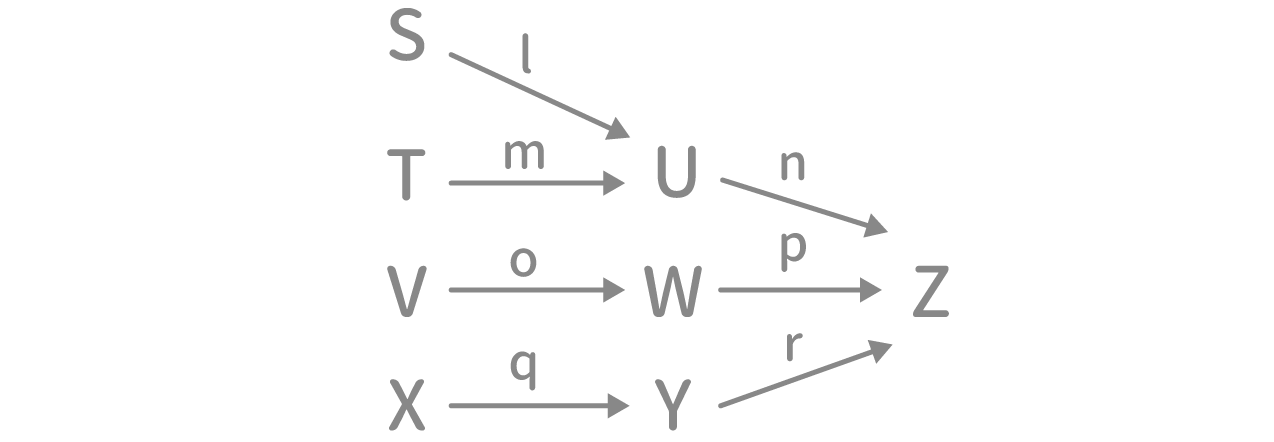
次のうち、正しい数式はどれか。
ア Z = mnT + opV + qrX
イ Z = nU + pW + rY
ウ Z = (l + n)S + (m + n)T + opV + qrX
A アだけ
B イだけ
C ウだけ
D アとイの両方
E アとウの両方
F イとウの両方
G アとイとウのすべて
H 正しい数式はない
유형14-2
次の図は、V会場とX会場からZ会場に進んだ人を表したものである。
(基本ルールは省略します。)
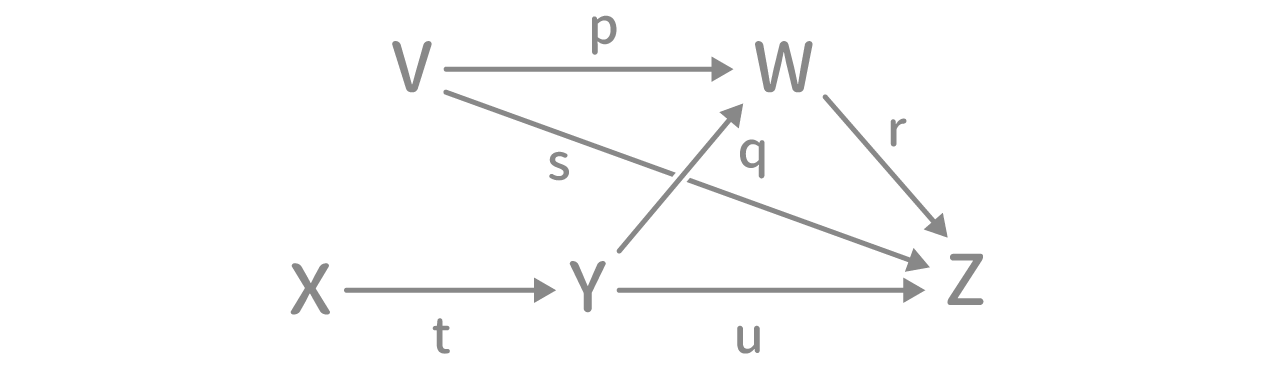
p = 0.2、q = 0.5、r = 0.1、s = 0.3、t = 0.5、u = 0.2である。X会場にいた人が160人、W会場に進んだ人が60人のとき、V会場にいた人は何人か。
A 100人
B 120人
C 140人
D 160人
E 180人
F 200人
G 220人
H 240人
SPI 비언어 문제 모음 사이트
https://saisokuspi.com/higengo
【2024年卒】SPI非言語 例題・問題をイラストで超分かりやすく解説! 【Study Pro】
Copyright (c) - SPI無料学習サイト|StudyPro - All Rights Reserved
saisokuspi.com
이번에도 참고 사이트를 소개하면서 글을 마친다.
미처 못 다룬 유형은 다음 포스팅에서 살펴보도록 하겠다.

'일본 취업 준비' 카테고리의 다른 글
| 일본 취업 준비기(6) SPI 비언어(계산) 문제 유형 살펴보기 4 (0) | 2023.01.28 |
|---|---|
| 일본 취업 준비기(6) SPI 비언어(계산) 문제 유형 살펴보기 3 (0) | 2023.01.24 |
| 일본 취업 준비기(6) SPI 비언어(계산) 문제 유형 살펴보기 1 (2) | 2023.01.16 |
| 일본 취업 준비기(5) SPI 비언어(추론) 문제 유형 살펴보기 (0) | 2023.01.12 |
| 일본 취업 준비기(4) SPI 언어 파트 문제 유형 살펴보기 (0) | 2023.01.05 |